Answer:
Since stress is greater than ultimate strength, the wire will break.
Explanation:
The titanium wire is experimenting an axial load. Ultimate strength equals
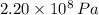 . The wire shall break if and only if stress is at least equal to ultimate strength. The equation for axial stress (
. The wire shall break if and only if stress is at least equal to ultimate strength. The equation for axial stress (
 ), measured in pascals, in the wire with circular cross-section is:
), measured in pascals, in the wire with circular cross-section is:
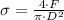 (1)
(1)
Where:
 - Axial force, measured in newtons.
- Axial force, measured in newtons.
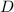 - Cross-section diameter, measured in meters.
- Cross-section diameter, measured in meters.
Please notice that axial force is the weight of the man hanging from wire.
If we know that
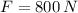 and
and
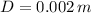 , then the axial stress experimented by the titanium wire is:
, then the axial stress experimented by the titanium wire is:

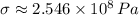
Since stress is greater than ultimate strength, the wire will break.