Question

Some mass m of gas initially at atmospheric pressure and room temperature (275k) undergoes a reversible transformation characterized by that equation T^2P= constant . The final pressure is Pf. Find the expression for the final work done.

Answer 1

The expression for the final work done is given by W = (constant/
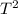`T^2`)(Vf - Vi), where constant is a constant value, T is the temperature, and Vi and Vf are the initial and final volumes, respectively.

The equation given,
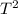`T^2`P = constant, represents a reversible transformation of a gas. To find the expression for the final work done, we can use the ideal gas law and the concept of work done by a gas.

First, let's rearrange the given equation to solve for pressure (P) in terms of temperature (T):

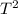`T^2`P = constant

P = constant/
`T^2`

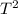
Next, let's consider the ideal gas law, which states:

PV = nRT

In this case, the mass of the gas (m) is given, so we can rewrite the ideal gas law as:

PV = (m/M)RT

where M is the molar mass of the gas.

Now, we can substitute the expression for pressure (P) from the rearranged equation into the ideal gas law:

(constant/
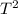`T^2`)V = (m/M)RT

To find the final work done, we need to calculate the difference between the initial and final volumes. Let's assume the initial volume is Vi and the final volume is Vf.

The work done by a gas can be expressed as:

W = PΔV

where ΔV is the change in volume.

Using the ideal gas law, we can express the change in volume as:

ΔV = (m/M)RTf - (m/M)RTi

Substituting the expression for pressure (P) into the work equation and simplifying, we get:

W = (constant/
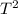`T^2`)(Vf - Vi)

In summary, the expression for the final work done is:

W = (constant/
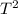`T^2`)(Vf - Vi)