To find the mass of ice that melted, we can use the principle of conservation of energy and the specific heat equation:
![\[ Q_{\text{cup}} + Q_{\text{water}} + Q_{\text{ice}} = 0 \]](https://img.qammunity.org/2024/formulas/physics/college/w3nkjaqtha7au1wiig9d6cbphvmsj9bm0u.png)
where
 is the heat absorbed or released, and the specific heat equation is
is the heat absorbed or released, and the specific heat equation is
 , where
, where
 is the mass,
is the mass,
 is the specific heat, and
is the specific heat, and
 is the temperature change.
is the temperature change.
Let's calculate each term:
1. Heat gained by the cup
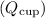 :
:
![\[ Q_{\text{cup}} = m_{\text{cup}}c_{\text{iron}}\Delta T_{\text{cup}} \]](https://img.qammunity.org/2024/formulas/physics/college/j3vi6ujdcjz1fxx9z4m1g5ji58wl4bi4kk.png)
2. Heat gained by the water
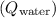 :
:
![\[ Q_{\text{water}} = m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/68819xuhs5gnfahoqpj0o2kfptlwskz2dn.png)
3. Heat lost by the melted ice
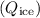 :
:
![\[ Q_{\text{ice}} = m_{\text{melt}}L_{\text{fusion}} \]](https://img.qammunity.org/2024/formulas/physics/college/r6n5d3f539453gv885g1io840mmq11262w.png)
Setting
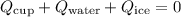 , we can solve for
, we can solve for
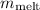 .
.
To calculate the mass of ice that melted
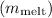 , we'll use the principle of conservation of energy and the specific heat equation:
, we'll use the principle of conservation of energy and the specific heat equation:
![\[ Q_{\text{cup}} + Q_{\text{water}} + Q_{\text{ice}} = 0 \]](https://img.qammunity.org/2024/formulas/physics/college/w3nkjaqtha7au1wiig9d6cbphvmsj9bm0u.png)
1. Heat gained by the cup
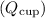 :
:
![\[ Q_{\text{cup}} = m_{\text{cup}}c_{\text{iron}}\Delta T_{\text{cup}} \]](https://img.qammunity.org/2024/formulas/physics/college/j3vi6ujdcjz1fxx9z4m1g5ji58wl4bi4kk.png)
![\[ Q_{\text{cup}} = (0.462 \ \text{kg})(412 \ \text{J/(kg K)})(-51.8 \ \text{°C}) \]](https://img.qammunity.org/2024/formulas/physics/college/phtxelrpiw46pem0e5wm3v72qezkkaa6o5.png)
2. Heat gained by the water
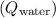 :
:
![\[ Q_{\text{water}} = m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/68819xuhs5gnfahoqpj0o2kfptlwskz2dn.png)
![\[ Q_{\text{water}} = (0.23 \ \text{kg})(4186 \ \text{J/(kg K)})(-51.8 \ \text{°C}) \]](https://img.qammunity.org/2024/formulas/physics/college/lfp9g0x6z2urf7sg7esqrwk1wnuwsg9a8s.png)
3. Heat lost by the melted ice
 :
:
![\[ Q_{\text{ice}} = m_{\text{melt}}L_{\text{fusion}} \]](https://img.qammunity.org/2024/formulas/physics/college/r6n5d3f539453gv885g1io840mmq11262w.png)
![\[ Q_{\text{ice}} = m_{\text{melt}}(334000 \ \text{J/kg}) \]](https://img.qammunity.org/2024/formulas/physics/college/gq5g0sg72lfl1getixuapun1cr4ick0qvf.png)
Now, plug these values into the conservation of energy equation and solve for
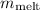 :
:
![\[ (0.462 \cdot 412 \cdot -51.8) + (0.23 \cdot 4186 \cdot -51.8) + (m_{\text{melt}} \cdot 334000) = 0 \]](https://img.qammunity.org/2024/formulas/physics/college/23b8w2mvbf4jau71hasidzfb8wwxrlvoyq.png)
After solving, we get
 . Therefore, approximately 0.084 kg of ice melted.
. Therefore, approximately 0.084 kg of ice melted.