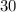Answer:
Explanation:
1. Approach
First, use the Pythagorean theorem to solve for the hypotenuse of the given right triangle. Then find the perimeter by adding up the values of all the sides. The problem then has the lengths of the legs doubled. When the legs undergo a scaling factor, the hypotenuse and perimeter undergo the same scaling factor. Here, the legs are doubled, hence the hypotenuse and the perimeter are also doubled. Finally, subtract the new perimeter from the original perimeter.
2. Find the original hypotenuse
Remember the Pythagorean theorem states;
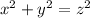
Where (a) and (y) are the legs (or the sides adjacent to the right angle), and (z) is the hypotenuse or the side opposite to the right angle.
Substitute in the given value and solve,
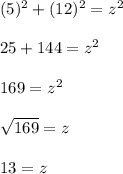
3.Find the perimeter of the original triangle
To find the perimeter of a polygon, one must add up the lengths of all the sides.
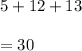
4. Find the new perimeter
In a right triangle, when both legs undergo a scaling factor, the hypotenuse also has the same change, and the perimeter also undergoes the same change. In this case, the length of the legs is doubled, therefore, the hypotenuse and the perimeter are also doubled.
New hypotenuse;

New perimeter;
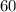
5. Find the difference
Now all that is left is to subtract the new perimeter from the original perimeter;
(New_perimeter) - (original_perimeter)
=
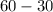
=