Question

What is the answer to this screenshot

Answer 1

The correct solutions are (5,2) and (6,-1), making the correct answer (c).

The given linear inequalities are:

`\(-3x + y < 1\)`

`\(x < 4\)`

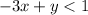
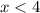
Let's evaluate the given answer choices:

a. (-1,4) and (-2,1):

For (-1,4):

`\[ -3(-1) + 4 = 3 + 4 = 7 \]`

The first inequality is not satisfied (7 is not less than 1). Therefore, (-1,4) is not a solution.

For (-2,1):

`\[ -3(-2) + 1 = 6 + 1 = 7 \]`

The first inequality is not satisfied (7 is not less than 1). Therefore, (-2,1) is not a solution.

b. (1,1) and (3,3):

For (1,1):

`\[ -3(1) + 1 = -2 \]`

The first inequality is satisfied (-2 is less than 1).

For (3,3):

`\[ -3(3) + 3 = -6 \]`

The first inequality is satisfied (-6 is less than 1).

c. (5,2) and (6,-1):

For (5,2):

`\[ -3(5) + 2 = -13 \]`

The first inequality is satisfied (-13 is less than 1).

For (6,-1):

`\[ -3(6) - 1 = -19 \]`

The first inequality is satisfied (-19 is less than 1).

Therefore, the correct solutions are (5,2) and (6,-1), making the correct answer (c).