Answer:
A.) The sum will be an even integer.
Explanation:
The conjecture that can be made about the sum of two even integers and one odd integer is that the sum will be an even integer. This is because even integers are numbers that are divisible by 2, and odd integers are numbers that are not divisible by 2.
For example, consider the sum of the even integer 6 and the odd integer 7. The sum of these two numbers is
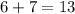 , which is an odd integer. However, if we add another even integer to the sum, such as 4, the resulting sum is
, which is an odd integer. However, if we add another even integer to the sum, such as 4, the resulting sum is
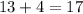 , which is an even integer. This shows that the sum of two even integers and one odd integer is always an even integer.
, which is an even integer. This shows that the sum of two even integers and one odd integer is always an even integer.
This conjecture can be proven using mathematical induction. We can start by showing that the sum of any two even integers and one odd integer is always an even integer. Then, we can assume that the sum of any n even integers and one odd integer is also an even integer. Finally, we can show that the sum of n+1 even integers and one odd integer is also an even integer, using the assumption that the sum of n even integers and one odd integer is even. This will prove that the conjecture is always true.