Question

A culture of bacteria has an initial population of 790 bacteria and doubles every 2 hours. Using the formula P, start subscript, t, end subscript, equals, P, start subscript, 0, end subscript, dot, 2, start superscript, start fraction, t, divided by, d, end fraction, end superscriptP

t
​
=P
0
​
⋅2
d
t
​

, where P, start subscript, t, end subscriptP
t
​
is the population after t hours, P, start subscript, 0, end subscriptP
0
​
is the initial population, t is the time in hours and d is the doubling time, what is the population of bacteria in the culture after 15 hours, to the nearest whole number?

Answer 1

The population of the culture of bacteria after 15 hours is 143005

How to determine the population after 15 hours

From the question, we have the following parameters that can be used in our computation:

`P_t = P_0 \cdot 2^(t)/(d)`

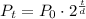
Also, we have

P(0) = 790

t = 15 hours

d = 2 hours i.e. the doubling time

Substitute the known values into the equation

`P(15) = 790 * 2^{(15)/(2)`

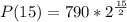
This gives

`P(15) = 790 * 2^{7.5`

Evaluate

P(15) = 143005

Hence, the population after 15 hours is 143005

Question

A culture of bacteria has an initial population of 790 bacteria and doubles every 2 hours.

Using the formula
`P_t = P_0 \cdot 2^(t)/(d)`

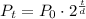
Where Pt is the population after t hours and P0 is the initial population, t is the time in hours and d is the doubling time, what is the population of bacteria in the culture after 15 hours, to the nearest whole number?