Question

a circle has a radius of 10 cm. what is the length of a tangent line segment whose endpoint is 12 cm away from the center of the circle

Answer 1

The length of the tangent line segment is approximately 6.63 cm (rounded to two decimal places).

To find the length of the tangent line segment to a circle from a point outside the circle, we can use the Pythagorean theorem.

The relationship is given by:

`{Tangent Length}^2` =
`{Distance from the Center}^2 - {Radius}^2`

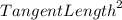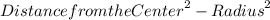
In this case, the radius of the circle is 10 cm, and the distance from the center to the endpoint of the tangent line is 12 cm. Let TL represent the tangent length:

TL^2 = 12^2 - 10^2

TL^2 = 144 - 100

TL^2 = 44

Now, take the square root of both sides to find the tangent length:

`\[ TL = √(44) \]`

So, the length of the tangent line segment is approximately 6.63 cm (rounded to two decimal places).