To solve a system of equations using substitution, you can start by solving one of the equations for one of the variables, such as x or y. For example, in this case, we can solve the first equation for x by subtracting y from both sides, like this:
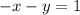
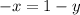
Now that we have an expression for x in terms of y, we can substitute that expression into the second equation to solve for y. When we do that, we get:
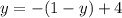

Now we can rearrange the terms on the right-hand side to make it easier to solve for y:
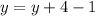
And when we combine the y terms on the left-hand side, we get:
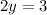
Finally, we can solve for y by dividing both sides by 2, like this:

Once we know the value of y, we can substitute it back into any of the original equations to solve for the other variable, x. In this case, if we substitute the value of y into the first equation, we get:
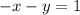
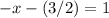
We can solve for x by rearranging the terms on the left-hand side and then dividing both sides by -1, like this:
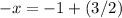
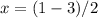
Therefore, the solution to the system of equations is x = -1 and y = 3/2.
It's important to check your solution by substituting the values of x and y into the original equations to make sure they work. For example, if we substitute x = -1 and y = 3/2 into the first equation, we get:
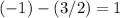
And if we substitute the same values into the second equation, we get:
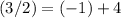
Both of these equations are true, which means our solution is correct.