Question

what is the present value of an ordinary annuity of $4,175 each year for eight years, assuming an opportunity cost of 12 percent?

Answer 1

To calculate the present value of an ordinary annuity of $4,175 each year for eight years with a 12% interest rate, use the formula PV =
`Pmt * [(1 - (1 + r)^-n) / r]`, where Pmt is the annual payment, r is the interest rate, and n is the number of years.

The question is asking to calculate the present value of an ordinary annuity.

An annuity is a series of equal payments made at regular intervals over a specified period.

To find the present value, we use the present value formula for an ordinary annuity:

PV =
`Pmt * [(1 - (1 + r)^-n) / r]`

Where:

PV is the present value of the annuity,

Pmt is the annual payment ($4,175),

r is the interest rate (12% or 0.12), and

n is the total number of payments (8 years).

Thus, by applying the values:

PV = $4,175 * [
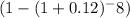`(1 - (1 + 0.12)^-8)` / 0.12]

Performing the calculations will give us the present value of the annuity.

The outcome of this calculation will allow us to understand what amount of money, if invested today at a 12% opportunity cost, would be equivalent to receiving $4,175 each year for eight years.