Question

A 50 kg bumper car with a 40 kg child and it is at rest when a 60 kg child in her own bumper car slams into it the collision last point1 seconds and the rubber bumpers are perfectly bouncy with no heating from the collision what is the force experienced by the first car

Answer 1

F = 99 v₂₀

v₂₀ = 1 m / s, F = 99 N

Step-by-step explanation:

In this exercise it is asked to find the force during the collision, for this we use the relationship between the momentum and the momentum of car 1

I = Δp

F t = p_f- p₀

F t = m (v_f -v₀) (1)

We must find the final speed of car 1, for this we define a system formed by the two cars, in this case the forces during the collision are internal and the moment is conserved

initial instant. Before the crash

p₀ = 0 + m₂ v₂₀

final instant. After the crash

p_f = m₁ v₁ + m₂ v_{2f}

the moment is preserved

p₀ = p_f

m₂ v₂₀ = m₁ v_{1f} + m₂ v_{2f} (2)

m₂ (v₂₀ - v_2f}) = m₁ v_{1f}

as the collision is elastic the kinetic energy is also conserved

K₀ = K_f

½ m₂ v₂₀² = ½ m₁ v_{1f}² + ½ m₂ v_{2f}²

m₂ (v₂₀² -v_{2f}²) = m₁ v_{1f}²

let's write our system of equations, using

a² - b² = (a + b) (a-b)

m₂ (v₂₀ - v_{2f}) = m₁ v_{1f}

m₂ (v₂₀ -v_{2f}) (v₂₀ + v_{2f}) = m₁ v_{1f}²

to solve we divide the equations

v₂₀ + v_{2f} = v_{1f}

with this we substitute in equation 2 and find the speed of each car, in this case we need the speed of car 1

m₂ v₂₀ = m₁ v_{1f} + m₂ (v_{1f}-v₂₀)

2m₂ v₂₀ = (m₁ + m₂) v_{1f}

v_{1f} =
`(2m_2)/(m_1+m_2) v_(2o)`

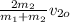
We substitute in the drive ratio of car 1

F t = m (v_f -v₀)

F = m₁ (\frac{2m_2}{m_1+m_2} v_{2o} - 0) / t

F =
`(2m_1 m_2 )/(m_1+m_2) \ (v_(2o))/(t)`

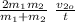
the mass of each car is the mass of the car plus the mass of the boy

m₁ = 50 +40 = 90 kg

m₂ = 50 +60 = 110 kg

time is t = 1

we substitute the values

F =
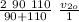`( 2\ 90 \ 110)/(90+110) \ (v_(2o))/(1)`2 90 100/90 + 110 vo2 / 1

F = 99 v₂₀

The value of the initial velocity of car 2 is not indicated in the problem, if this velocity is known it can be included and the force value is obtained, suppose that the initial velocity v₂₀ = 1 m / s

F = 99 N