Question

A ship at A is to sail to C, 56 km north and 258 km east of A. After sailing N25°10'E for 120 mi to P, the ship is headed toward C. Find the distance of P from C and the required course to mean C

Answer 1

The distance from P to C is approximately 277 km, and the required course to reach C from P is N58°50'E. The ship should steer a course of N64°50'E to reach point C from point P.

The ship initially sails 56 km north and 258 km east from A to reach point C. After sailing N25°10'E for 120 miles, the ship arrives at point P. To find the distance from P to C, we can use the Pythagorean theorem, treating the northward and eastward distances as the legs of a right-angled triangle. The distance PC is the hypotenuse, and it can be calculated as follows:

`PC = \sqrt{(258 km)^(2) + ( 56 km)^(2)`

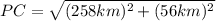
After the calculation, PC is approximately 277 km. To determine the required course from P to C, we use trigonometry. The ship is initially heading N25°10'E, and to reach C, it must change its course. The angle between the eastward direction and the line PC is the angle we're looking for. Subtracting this angle from 90° gives us the required course. Therefore,

Required course= 90°−(25°10′)=64°50′

In summary, the distance from P to C is approximately 277 km, and the required course to reach C from P is N64°50'E.