Question

A medical investigation claims that the average number of infections per week at a hospital in southwestern pennsylvania is 16.3. a random sample of 10 weeks had a mean number of 17.7 infections. the sample standard deviation is 1.8. is there enough evidence to reject the investigator’s claim at α = 0.05 ?

Answer 1

There is evidence to suggest that the true average number of infections per week at the hospital is different from 16.3.

To test whether there is enough evidence to reject the investigator's claim, we can conduct a hypothesis test.

Given:

Population mean (μ) = 16.3

Sample mean (x) = 17.7

Sample standard deviation (s) = 1.8

Sample size (n) = 10

Significance level (α) = 0.05

We'll use a one-sample t-test since the population standard deviation is not provided.

The null hypothesis (H₀) is that the true average number of infections per week at the hospital is 16.3.

The alternative hypothesis (H₁) is that the true average number of infections per week at the hospital is not 16.3.

The formula for the t-test is:

t=
`(x-\mu)/((s)/(√(n) ) )`

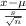
​Where:

x = Sample mean

μ = Population mean

s = Sample standard deviation

n = Sample size

Let's calculate the t-statistic:

t=
`(17.7-16.3)/((1.8)/(√(10) ) )`​

t=
`(1.4)/((1.8)/(√(10) ) )`

​t ≈
`\frac{{1.4}}{{0.568}}}`

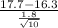
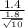
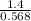
t≈2.465

Now, we need to compare the calculated t-value with the critical t-value at a 5% significance level with degrees of freedom (df) =

n−1=10−1=9.

You can use statistical tables or calculators to find the critical t-value. For α = 0.05 and df = 9, the critical t-value is approximately 2.262 (two-tailed test).

Since the calculated t-value (2.465) is greater than the critical t-value (2.262), we have enough evidence to reject the null hypothesis at α = 0.05. Therefore, there is evidence to suggest that the true average number of infections per week at the hospital is different from 16.3.