The expression
 simplifies to
simplifies to
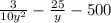 after distribution, simplification, and combining like terms.
after distribution, simplification, and combining like terms.
the expression
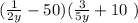 the distributive property.
the distributive property.
Given expression:

First, let's distribute
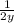 to both terms inside the second parenthesis, and then distribute
to both terms inside the second parenthesis, and then distribute
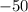 to both terms inside the second parenthesis:
to both terms inside the second parenthesis:
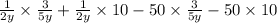
Now, perform the multiplication:

Simplify each term:

Combine like terms:
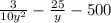
Hence, after simplification, the expression
 simplifies to
simplifies to
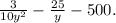
complete the question
Solve the binomial. (1/2y - 50)(3/5y + 10)