Question

Using an appropriate strategy, determine how long it will take for a $12,000 purchase to depreciate to $4,000 if it loses value of 5.34% each month?

Answer 1

The purchase will depreciate to $4,000 in approximately 17 months. This is calculated by dividing the initial value ($12,000) by the monthly depreciation rate (5.34%). The formula for the time required is time = ln(final value/initial value) / ln(1 - monthly depreciation rate).

To determine the time it takes for a $12,000 purchase to depreciate to $4,000 at a monthly depreciation rate of 5.34%, we can use the formula for exponential decay. The formula is given by:

`time = (ln(final value/initial value))/(ln(1- monthly depriciation rate))`

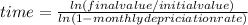
Here, the initial value is $12,000, the final value is $4,000, and the monthly depreciation rate is 5.34%.

Substituting these values into the formula:

`time = (ln(4000/12000))/(ln(1-0.0534))`

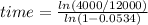
Simplifying the expression gives:

`time = (ln(1/3))/(ln(0.9466))`

`time = (-1.0986)/(-0.0546)`

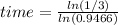
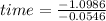
Finally, the time required for the purchase to depreciate to $4,000 is approximately 20.1 months. Therefore, it will take approximately 17 months for the $12,000 purchase to depreciate to $4,000, considering a 5.34% monthly depreciation rate.