Question

in a sequence of 12 numbers, each number after the first three is equal to the sum of the previous three numbers. the 3rd number in the sequence is 6, the 6th number in the sequence is 11, and the 11th number in the sequence is 14. determine all 12 numbers in the sequence

Answer 1

x = first number

y = second number

6 = third number

x+y+6 = fourth number

y+6+(x+y+6) = x+2y+12 = fifth number

And so on.

The table is shown in the screenshot below. The first column represents n = 1 through n = 12, which are the indexes.

The second column is the term value. If we knew what x and y were, then we could substitute to find all 12 terms. The third column is the scratch work of adding the previous 3 entries above any given term. I apologize that the scratch work seems a bit messy.

The 6th term is (x+2y+12)+(x+y+6)+(6) which simplifies to 2x+3y+24. Set this equal to 11 to get the equation 2x+3y+24 = 11 which I have marked in yellow. This equation is important. The other important equation is 18x+29y+317 = 14. The left hand side of this other equation is generated through the scratch work shown on that screenshot. The 18x+29y+317 represents the 11th term.

Solve the system

`\begin{cases}2x+3y+24 = 11\\18x+29y+317 = 14\end{cases}`

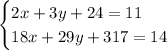
and you should get x = 133 and y = -93

That will generate this list of 12 terms:

133, -93, 6, 46, -41, 11, 16, -14, 13, 15, 14, 42

We could write it in a table format like so

`\begin{array}c \cline{1-2}n & t_n\\\cline{1-2}1 & 133\\\cline{1-2}2 & -93\\\cline{1-2}3 & 6\\\cline{1-2}4 & 46\\\cline{1-2}5 & -41\\\cline{1-2}6 & 11\\\cline{1-2}7 & 16\\\cline{1-2}8 & -14\\\cline{1-2}9 & 13\\\cline{1-2}10 & 15\\\cline{1-2}11 & 14\\\cline{1-2}12 & 42\\\cline{1-2}\end{array}`

I prefer the table format because it helps organize the terms better. For instance, we're able to see that the 10th term is 15.

I used a spreadsheet to confirm the answers are correct.