In a normal distribution of bonsai tree heights with a mean of 52 cm and a standard deviation of 10 cm, approximately 95% of trees fall between 32 cm and 72 cm in height.
To find the range within which 95% of the bonsai trees' heights lie, we'll use the properties of a normal distribution.
Given:
Mean height
 = 52 cm
= 52 cm
Standard deviation
 = 10 cm
= 10 cm
We'll use the formula for a normal distribution to determine the range within which 95% of the data falls, which is within approximately 2 standard deviations from the mean.
Calculate the interval:
Lower Limit:
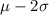
![\[ \text{Lower Limit} = 52 - 2 * 10 = 52 - 20 = 32 \text{ cm} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qwr23sw3vt5a022e07flcimnjesk2eptln.png)
Upper Limit:
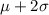
![\[ \text{Upper Limit} = 52 + 2 * 10 = 52 + 20 = 72 \text{ cm} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zgbl3n3hrhnxbix0p9d36tf7zbklzwa2zr.png)
Therefore, using this calculation, we've determined that 95% of the bonsai trees' heights fall within the range of 32 cm to 72 cm.
complete the question
If the mean height of bonsai trees is 52 cm with a standard deviation of 10 cm, 95% of the trees are between □ cm and □ cm.