Question

If $100000 is invested today in an account that earns interest at a rate of 20%, what is the value of the equal withdrawals that can be taken out of the account at the end of each of the next eight years if the investor plans to deplete the account at the end of time period?

A. $26060.
B. $28505.
C. $31030.
D. $34213.

Answer 1

The student's question asks for determining the equal annual withdrawals from an account with $100,000 initial investment at 20% interest rate over 8 years that would deplete the account. By using the annuity payout formula, the calculations show that the correct withdrawal amount is approximately $31,030 per year, which makes option C the correct answer.

The question involves calculating the equal withdrawals from an investment account over a period of 8 years based on an initial investment and a fixed interest rate.

To find the equal annual withdrawals that would deplete the account at the end of 8 years, we need to use the formula for the annuity payout.

This formula is based on the present value of an annuity formula:

PV = PMT ×
`((1 - (1 + r)^(-n)) / r)`

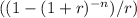
Where:

PV = Present Value of the annuity (the amount initially invested),

PMT = Periodic payment (annual withdrawal in this case),

r = Interest rate per period,

n = Number of periods.

For this question:

PV = $100,000,

r = 20% or 0.20,

n = 8.

To find PMT, we rearrange the formula:

PMT = PV /
`((1 - (1 + r)^(-n)) / r)`

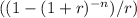
Substitute the given values:

PMT = $100,000 / ((1 - (1 + 0.20)^{-8}) / 0.20)

Solving this, we find:

PMT = $100,000 / ((1 -
`(1 + 0.20)^(-8))` / 0.20) = $31030 (approximately)

The correct answer is C. $31030.

The withdrawals of approximately $31,030 per year will deplete the account entirely at the end of 8 years.