Question

A person randomly selects one of six envelopes. Each envelope contains a check that the person gets to keep.

Determine the person's expectation if three envelopes contain a $534 check and three envelopes contain a $964 check.

Answer 1

The person's expectation, choosing among six envelopes with $534 and $964 checks equally distributed, is $749. This represents the average value they can anticipate receiving upon selection.

Given:

Three envelopes contain a $534 check.

Three envelopes contain a $964 check.

The expected value (E) is calculated as follows:

`\[ E = \text{Probability}_1 * \text{Value}_1 + \text{Probability}_2 * \text{Value}_2 + \ldots \]`

Let's denote:

`\( P_1 \)` as the probability of getting $534 check

`\( P_2 \)` as the probability of getting $964 check

`\( V_1 \)` as the value of the $534 check

`\( V_2 \)` as the value of the $964 check

Given:

`\( P_1 = (3)/(6) = (1)/(2) \)` (since 3 envelopes out of 6 contain $534 check)

`\( P_2 = (3)/(6) = (1)/(2) \)` (since 3 envelopes out of 6 contain $964 check)

`\( V_1 = $534 \)`

`\( V_2 = $964 \)`

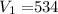
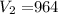
The expectation is calculated as:

`\[ E = P_1 * V_1 + P_2 * V_2 \]`

`\[ E = (1)/(2) * 534 + (1)/(2) * 964 \]`

`\[ E = 267 + 482 \]`

`\[ E = 749 \]`

Therefore, the person's expectation when selecting one envelope out of six is
`$749`. This is the average value they can expect to receive.