Question

In a certain​ study, women's heights are found to be approximately normally distributed with a mean of 65 inches and a standard deviation of 2.5 inches.

what would be the​ z-score for a woman who is 4 feet 10 inches ​tall?

Answer 1

The
`\( z \)`-score for a woman with a height of 4 feet 10 inches (58 inches) in a distribution with a mean of 65 inches and a standard deviation of 2.5 inches is -2.8.

To find the
`\( z \)`-score for a woman who is 4 feet 10 inches tall, first, convert this height to inches.

1 foot = 12 inches, so 4 feet =
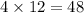`\( 4 * 12 = 48 \)`inches.

Adding the remaining 10 inches gives a total of
`\( 48 + 10 = 58 \)`inches.

to calculate the
`\( z \)`-score using the formula:

`\[ z = \frac{{\text{Observation} - \text{Mean}}}{{\text{Standard Deviation}}} \]`

Given:

Mean height
`(\( \mu \))`= 65 inches

Standard deviation
`(\( \sigma \))`= 2.5 inches

Observation = 58 inches

`\[ z = \frac{{58 - 65}}{{2.5}} \]`

`\[ z = \frac{{-7}}{{2.5}} \]`

`\[ z = -2.8 \]`

Therefore, the
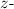`\( z \)-`score for a woman who is 4 feet 10 inches tall is -2.8.