Question

Use the distributive property and combine like terms to simplify: 1/5(4m 20)

Answer 1

Using the distributive property,
`\( (1)/(5)(4m + 20) \)` simplifies to
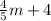`\( (4)/(5)m + 4 \)` by distributing
`\((1)/(5)\)` .

To simplify the expression
`\( (1)/(5)(4m + 20) \)` using the distributive property, distribute
`\((1)/(5)\)` to both terms inside the parentheses:

`\[ (1)/(5) * 4m + (1)/(5) * 20 \]`

Simplify each term separately:

`\[ (4)/(5)m + (20)/(5) \]`

Now, combine the like terms:

`\[ (4)/(5)m + 4 \]`

So,
`\( (1)/(5)(4m + 20) \)` simplifies to
`\( (4)/(5)m + 4 \)`.

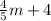In summary, using the distributive property and combining like terms, the simplified expression is
`\( (4)/(5)m + 4 \)`.

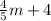Que. Use the distributive property and combine like terms to simplify: 1/5(4m + 20)