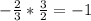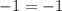Answer:
Lines A and C are parallel
Lines B and D are perpendicular
Explanation:
Given
See attachment for lines A to D
Required
Determine the parallel and perpendicular lines
To start with, we calculate the slope of each line.
Line A
The points on line A are:
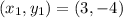

Calculate the slope (m)

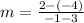
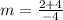
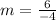
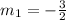
Line B


Calculate the slope (m)



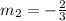
Line C
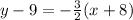
Open bracket
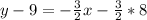
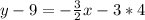
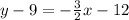
Make y the subject

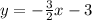
The slope intercept of an equation is:

Where
By comparison:
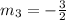
Line D
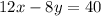
Subtract 12x from both sides
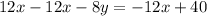

Divide through by -8
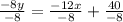
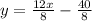
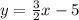
The slope intercept of an equation is:

Where
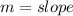
By comparison:
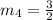
So, the slopes of the lines are:
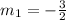
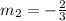
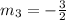
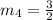
Lines with the same slope are parallel.
So:
Lines A and C with slope of
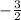 are parallel
are parallel
Lines with the following relationship are perpendicular:
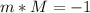
Lines B and D are perpendicular because: