Question

The temperature of an object, T, in degrees Fahrenheit after t minutes is represented by the equation T(t)=68e⁽⁻⁰.⁰¹⁷⁴ᵗ⁾+72. How long will it take an object to get to 86 degrees? Round your answer to three decimal places.

____ minutes

Answer 1

Rounded to three decimal places, it will take approximately 176.747 minutes for the object to reach 86 degrees Fahrenheit.

To find when the temperature reaches 86 degrees Fahrenheit, you can set up the equation and solve for t in the equation T(t)=86.

Given:

`T(t) =68e^(-0.0174t) + 72`

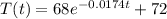
We want to find t when T(t)=86:

`82 =68e^(-0.0174t) + 72`

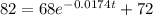
First, isolate the exponential term:

`68e^(-0.0174t)= 86-72\\68e^(-0.0174t)= 14`

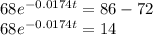
Next, solve for
`e^(-0.0174t)`:

`e^(-0.0174t)=(14)/(68) \\e^(-0.0174t)=(7)/(34)`

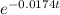​Now, take the natural logarithm of both sides to solve for t:

ln(e−0.0174t )=ln( 7/34 )

−0.0174t=ln( 7/34 )

Finally, solve for t:

t= ln( 7/34 )/ −0.0174

t≈176.747

Rounded to three decimal places, it will take approximately 176.747 minutes for the object to reach 86 degrees Fahrenheit.