Question

The number 40 could be written as the product of its prime factor 40=2x2x2x5 write 60 as a product of its prime factor write in order smallest to larges

Answer 1

The prime factorization of 60 is
`\(2 * 2 * 3 * 5\)`, arranged in ascending order, which is
`\(2 * 2 * 3 * 5\).`

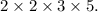
To find the prime factorization of 60, start by dividing the number by the smallest prime number, which is 2, and continue the process until the quotient becomes 1.

`\[ 60 \]`

Since 60 is even, divide it by 2:

`\[ 60 / 2 = 30 \]`

Now, 30 is still even, divide it by 2 again:

`\[ 30 / 2 = 15 \]`

15 is not divisible by 2, try the next prime number, which is 3:

`\[ 15 / 3 = 5 \]`

5 is a prime number itself, so the prime factorization is complete:

`\[ 60 = 2 * 2 * 3 * 5 \]`

In ascending order:

`\[ 60 = 2 * 2 * 3 * 5 \]`