To solve
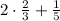 :
:
Convert
 to an improper fraction:
to an improper fraction:

Add
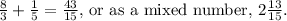
let's solve
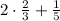 step by step.
step by step.
First, convert the mixed number to improper fractions:
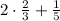
To convert
 to an improper fraction, multiply the whole number (2) by the denominator (3) and add the numerator (2), then place it over the denominator:
to an improper fraction, multiply the whole number (2) by the denominator (3) and add the numerator (2), then place it over the denominator:

Now the equation becomes:
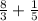
To add these fractions, find a common denominator, which is 15 in this case:
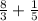
Multiply the first fraction by
 to make the denominators the same:
to make the denominators the same:

Now add the fractions:
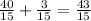
Therefore,
 n, which as a mixed number is
n, which as a mixed number is
