Question

In triangle FAB , FA = 2 x + 7, AB = x + 12, and FB = 4 x .

What must be true about the value of x ?

Answer 1

The value of x must be greater than 1.

To solve this problem

We may make use of the triangle's characteristics and the provided side length data.

Any two side's length added together must be more than the third side's length in a triangle. The Triangle Inequality Theorem is the name given to this.

We can write the following inequalities using triangle FAB and the Triangle Inequality Theorem:

1
`. FA + AB > FB`

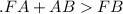
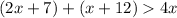
`(2x + 7) + (x + 12) > 4x`

2.
`FA + FB > AB`

`(2x + 7) + 4x > x + 12`

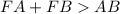
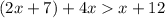
3.
`AB + FB > FA`

`(x + 12) + 4x > 2x + 7`

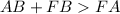
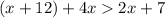
Simplifying these inequalities, we get:

1.
`3x + 19 > 4x`

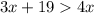
2
`. 6x + 7 > x + 12`

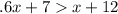
3
`. 5x + 12 > 2x + 7`

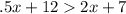
Finding the value of x so that it fulfills each of the three inequality

We need to solve them one by one:

Now, let subtracting 3x from both sides, we get:

`19 > x`

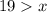
Secondly, let subtracting x from both sides, we get:

`5x > 5`

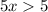
Dividing both sides by 5 (since x cannot be zero), we get:

`x > 1`

Lastly, let subtracting 2x from both sides, we get:

`3x > -5`

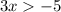
Dividing both sides by 3 (since x cannot be zero), we get:

`x > -5/3`

We may determine that x must be greater than 1 and greater than -5/3 by taking into account the solutions to all three inequalities.

So, the value of x must be greater than 1.