Question

Write an equation for the hyperbola with vertices at (−2,0) and (2,0), and passing through (10,1).

An equation for the hyperbola is (Simplify your answer: Type your answer in standard form . Use integers or fractions for any numbers in the equation )

Answer 1

The equation of the hyperbola is
`x^2 / 4 - y^2 / 9 = 1.\\`

1. Identify key parameters:

Vertices: (-2, 0) and (2, 0) - These points lie on the x-axis, so the transverse axis is horizontal.

Point on the hyperbola: (10, 1) - This point helps us determine the distance between the center and a focus (foci are equidistant from the center).

2. Find the distance between the center and a focus (eccentricity):

The center of the hyperbola is the midpoint of the segment connecting the vertices: (0, 0).

The distance between the center and a vertex is 2 units (absolute difference in x-coordinates).

Since the foci are equidistant from the center, the distance between the center and a focus is also 2 units.

Therefore, the eccentricity (e) of the hyperbola is
`√(1 + (2^2/0^2)) = √5.`

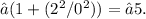
3. Find the distance between the center and a point on the hyperbola:

The distance between the center (0, 0) and the point (10, 1) is
`√(10^2 + 1^2) = √101.`

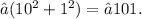
4. Use the standard equation of a hyperbola:

Since the transverse axis is horizontal, the standard equation of the hyperbola is:

`(x - h)^2 / a^2 - (y - k)^2 / b^2 = 1`

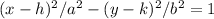
Where:

(h, k) is the center coordinates: (0, 0)

a is the distance between the center and a focus (2 units)

b is related to a and the eccentricity (e) by the equation:
`b^2 = a^2 * (e^2 - 1)`

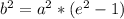
5. Substitute and solve for b:

`b^2 = 2^2 * (√5^2 - 1) = 9`

b = √9 = 3

6. Write the final equation:

`(x - 0)^2 / 2^2 - (y - 0)^2 / 3^2 = 1`

Simplifying:

`x^2 / 4 - y^2 / 9 = 1`

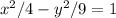
Therefore, the equation of the hyperbola is
`x^2 / 4 - y^2 / 9 = 1.\\`