There are 10 different ways to select 3 cards from a set of 5 different cards.
The number of ways to select k items from a set of n items is given by the combination formula, which is denoted as
C(n,k) or
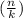
For your case of selecting 3 cards from 5 different cards, you'd use the combination formula:
C(5,3)= 5!/ 3!(5−3)!
Here's how it works:
5! means 5 factorial, which is 5×4×3×2×1.
3! means 3 factorial, which is 3×2×1.
5−3=2, so 2! is 2×1.
Plugging these values into the formula:
C(5,3)= 5!/ 3!(5−3)! = 5×4×3×2×1/ 3×2×1×2×1 = 120/ 6×2 = 120/ 12 =10
So, there are 10 different ways to select 3 cards from a set of 5 different cards.