Question

At the times zero there will be 10.0 g of tungston-187 if the half life is 23.9 hours how much will be present at the end of exactly one day

Answer 1

At the end of exactly one day, there will be approximately 5.01 grams of tungsten-187 remaining, given the half-life of 23.9 hours.

The decay of a radioactive substance follows an exponential decay equation given by:

`\[ N(t) = N_0 * \left((1)/(2)\right)^{\frac{t}{T_{\text{1/2}}}} \]`

where:

-
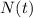`\( N(t) \)` is the quantity of the substance at time
`\( t \)`,

-
`\( N_0 \)` is the initial quantity of the substance,

-
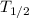`\( T_{\text{1/2}} \)` is the half-life of the substance.

In this case, for tungsten-187,
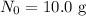`\( N_0 = 10.0 \) g` and
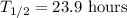`\( T_{\text{1/2}} = 23.9 \) hours`. After one day
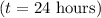`(\( t = 24 \) hours)`, we can substitute these values into the equation:

`\[ N(24) = 10.0 * \left((1)/(2)\right)^{(24)/(23.9)} \]`

Calculating the quantity of tungsten-187
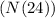`(\(N(24)\))` at the end of exactly one day using the exponential decay equation:

`\[ N(24) = 10.0 * \left((1)/(2)\right)^{(24)/(23.9)} \]`

`\[ N(24) = 10.0 * \left((1)/(2)\right)^(1.00209) \]`

`\[ N(24) \approx 10.0 * 0.500786 \]`

`\[ N(24) \approx 5.00786 \, \text{g} \]`

So, at the end of exactly one day, there will be approximately 5.01 grams of tungsten-187 remaining, given the half-life of 23.9 hours.