Question

A bakery sells apple pies for $12 each, and sells an average of 40 apple pies per day. The owner estimates that for each $0.50 increase in price, the average sales will decrease by one pie a day.

Suppose there have been x increases of $0.50 in the price of an apple pie above the initial price of $12.

Write down an expression for the price, $P, of an apple pie after x increases of $0.50 above the initial price of $12.

Answer 1

a. The expression for the price (SP) after x $0.50 increases is SP = 12 + 0.50x. b. The number of apple pies sold per day is 40 - x. c. The estimated revenue function is R = (12 + 0.50x) × (40 - x). d. To maximize revenue, the bakery owner should charge $16 per apple pie after 8 price increases of $0.50.

a. Expression for the Price (SP):

- The initial price of an apple pie is $12.

- For each $0.50 increase in price (x) increases), the new price is 12 + 0.50x.

- Therefore, the expression for the price, SP, after x increases of $0.50 is: SP = 12 + 0.50x.

b. Number of Apple Pies Sold (Q):

- The average sales decrease by one pie for each $0.50 increase.

- So, the number of apple pies sold per day is 40 - x.

c. Estimated Revenue Function (R):

- Revenue (R) is the product of price and quantity.

-
`\(R = SP * Q\)`

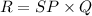
- Substituting the expressions from parts (a) and (b):
`\(R = (12 + 0.50x) * (40 - x)\)`.

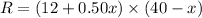d. Maximizing Revenue:

- To find the sale price that maximizes revenue, differentiate R with respect to x and set it equal to zero.

-
`\(R' = (dR)/(dx) = 0\)`

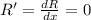
- Solve for x and substitute it back into the expression for the price (SP) to find the optimal sale price. The value of (x) represents the number of price increases that maximizes revenue.

- Differentiate the revenue function (R) with respect to (x):

`\[ R' = (dR)/(dx) = (40 - x) * 0.50 - (12 + 0.50x) \]`

- Set (R') equal to zero and solve for (x):

`\[ (40 - x) * 0.50 - (12 + 0.50x) = 0 \] \[ 20 - 0.50x - 12 - 0.50x = 0 \] \[ -x = -8 \] \[ x = 8 \]`

- The optimal value for (x) is 8, which means the bakery should increase the price (8) times by $0.50.

- Substitute (x = 8) into the expression for the price (SP):

SP = 12 + 0.50(8) = 16

- Therefore, the bakery owner should charge $16 per apple pie to maximize the revenue from apple pie sales.

The complete question is:

A bakery sells apple pies for $12 each and sells an average of 40 apple pies per day. The owner estimates that for each $0.50 increase in price, the average sales will decrease by one pie a day. Suppose there have been x increases of $0.50 in the price of an apple pie above the initial price of $12. a. Write down an expression for the price, SP, of an apple pie after x increases of $0.50 above the initial price of $12. b Write down the number of apple pies sold per day in terms of x. c. Find a function that gives the estimated revenue, R. from apple pie sales in terms of x. d Use the revenue function to find the sale price the bakery owner should charge to maximize the revenue from apple pie sales.