Question

A $23,000, 8.4% bond redeemable at par is purchased 5.5 years before maturity to yield 9.2% compounded semi-annually. If the bond interest is payable semi-annually, what is the purchase price of the bond?

The purchase price of the bond is $ ....
(Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as needed.)

Answer 1

The purchase price of the bond, with a face value of $23,000, 8.4% coupon rate, and 5.5 years to maturity, is approximately $27,820.53 when purchased to yield 9.2% compounded semi-annually.

To calculate the purchase price of the bond, you can use the present value formula for bonds:

`\[ P = \frac{C * \left(1 - \frac{1}{{(1 + r/n)^(nt)}}\right)}{(r)/(n)} + \frac{F}{{(1 + r/n)^(nt)}} \]`

Where:

- P is the purchase price,

- C is the semi-annual coupon payment,

- r is the semi-annual interest rate,

- n is the number of compounding periods per year,

- t is the total number of compounding periods until maturity, and

- F is the face value of the bond.

In this case, the bond has a face value (F) of $23,000, a semi-annual coupon rate (C) of
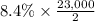`\( 8.4\% * (23,000)/(2) \)`, a semi-annual yield (r) of
`\( (9.2\%)/(2) \)`, and a time to maturity (t) of 5.5 years with n = 2 (compounded semi-annually).

Let's plug in the values:

`C = 0.084 * (23,000)/(2) \\ r = (9.2\%)/(2)`

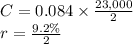
n = 2

t = 5.5 × 2

F = 23,000

Now calculate P:

`\[ P = \frac{C * \left(1 - \frac{1}{{(1 + r/n)^(nt)}}\right)}{(r)/(n)} + \frac{F}{{(1 + r/n)^(nt)}} \]\[ P = \frac{(0.084 * (23,000)/(2)) * \left(1 - \frac{1}{{(1 + (0.092)/(2))^(2 * 5.5)}}\right)}{(0.092)/(2)} + \frac{23,000}{{(1 + (0.092)/(2))^(2 * 5.5)}} \]`

`\[ P \approx \frac{(966) * \left(1 - \frac{1}{{(1.046)^(11)}}\right)}{0.046} + \frac{23,000}{{(1.046)^(11)}} \]\[ P \approx ((966) * \left(1 - (1)/(1.669)\right))/(0.046) + (23,000)/(1.669) \]\[ P \approx ((966) * (0.669)/(1.669))/(0.046) + 13,759.832 \]`

`\[ P \approx (647.154)/(0.046) + 13,759.832 \]\[ P \approx 14,060.699 + 13,759.832 \]\[ P \approx 27,820.531 \]`

Therefore, the purchase price of the bond is approximately $27,820.53.