Question

Let f be defined on the interval (0,1) by f(x)=2x+1. Derive two different Fourier series which each give a representation of f valid on the interval (0,1) at least.

Answer 1

The Fourier series of f(x)=2x+1 on (0,1) has two representations. The first is a cosine series, where a₀ =1, aₙ =0, and bₙ =4/nπ for odd n. The second is a sine series, with aₙ =0 and bₙ =2/nπ for odd n. Both series converge to f(x) on (0,1).

The Fourier series of f(x)=2x+1 on the interval (0,1) can be represented using cosine and sine series. For the cosine series, the coefficients are given by a₀ =1, aₙ =0, and bₙ = 4/nπ​ for odd n. This series converges to f(x) on (0,1). Similarly, the sine series has coefficients aₙ =0 and bₙ = 2/nπ for odd n, and it also converges to f(x) on (0,1). The general form of the Fourier series is expressed as:

`f(x) = {a_0} + \sum_(n=1)^(\infty) \left( a_n \cos \left( (2n\pi x)/(T) \right) + b_n \sin \left( (2n\pi x)/(T) \right) \right)`

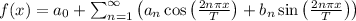
Where, T is the period of the function. In this case, the period is 1, as the function is defined on the interval (0,1). The coefficients aₙ and bₙ are determined based on the function being represented. For the given function f(x)=2x+1, the specific values of a₀, aₙ , and bₙ for the cosine and sine series were provided earlier. Both series provide an accurate representation of f(x) on the interval (0,1), showcasing the versatility of Fourier series in approximating a wide range of functions.