Question

Find the area of the parallelogram with consecutive vectors a(1,3,-2)b(2,1,4)and c(-3,1,6)

Answer 1

The area of the parallelogram formed by the vectors a, b, and c is
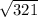`√(321)` square units.

To find the area of the parallelogram formed by the vectors a, b, and c, you can use the cross product of two adjacent vectors.

The magnitude of the cross product gives the area of the parallelogram.

Given two vectors u and v, the cross product u×v is given by:

`u * v= \left[\begin{array}{ccc}i&j&k\\u_1&u_2&u_3\\v_1&v_2&v_3\end{array}\right]`

In this case, the vectors a and b are adjacent sides of the parallelogram. Let's calculate the cross product a×b:

`a * b = \left[\begin{array}{ccc}i&j&k\\1&3&-2\\2&1&4\end{array}\right]`

Expanding the determinant, we get:

a×b=i(3⋅4−(−2)⋅1)−j(1⋅4−2⋅(−2))+k(1⋅1−2⋅3)

Simplifying further:

a×b=14i+10j−5k

Now, the magnitude of this cross product gives the area of the parallelogram:

Area= | a × b|=
`√(14^2 + 10^2 +(-5)^2)`

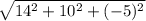
Calculating this, we get:

Area=
`√(196+ 100 +25)`=
`√(321)`

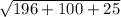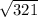
So, the area of the parallelogram formed by the vectors a, b, and c is
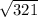`√(321)` square units.