Question

Evaluate f(x)=2x+3,g(x)=-x²+5,f°g

Answer 1

The composition
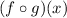`\((f \circ g)(x)\)` is
`\(2x^2 - 13\)`, obtained by substituting
`\(x^2 - 5\)` from g(x) into f(x). The expression represents the result of applying both functions f and g consecutively.

The composition
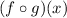`\((f \circ g)(x)\)`, also denoted as f(g(x)), involves substituting the expression for g(x) into f(x). Here's the computation:

`\[ g(x) = x^2 - 5 \]`

Now, substitute g(x) into f(x):

`\[ f(g(x)) = f(x^2 - 5) \]`

Now, substitute
`\(x^2 - 5\)` into f(x):

`\[ f(x^2 - 5) = 2(x^2 - 5) - 3 \]`

Simplify the expression:

`\[ (f \circ g)(x) = 2x^2 - 10 - 3 \]`

Combine like terms:

`\[ (f \circ g)(x) = 2x^2 - 13 \]`

So, the composition
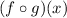`\((f \circ g)(x)\)` is a quadratic function
`\(2x^2 - 13\)` obtained by first applying the function
`\(g(x) = x^2 - 5\)` to the variable x and then applying the function f(x) = 2x - 3 to the result.