Question

Evaluate ∂u/∂z at (x,y,z)=(5,2,5) for the function u(p,q,r)=p²q²−r;p=y−z,q=x+z,r=x+y.

a. −420
b. 390
c. 1560
d. 780

Answer 1

The evaluation of ∂u/∂z at (5, 2, 5) for the function u(p, q, r) = p²q² − r yields a value of 780. Therefore, the correct answer is d. 780.

To find ∂u/∂z, we need to differentiate the function u with respect to z while treating x and y as constants. The given function is
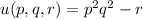`\(u(p, q, r) = p^2q^2 - r\)`, where p = y - z, q = x + z, and r = x + y.

Let's calculate the partial derivatives:

`\[ (\partial u)/(\partial z) = (\partial u)/(\partial p) (\partial p)/(\partial z) + (\partial u)/(\partial q) (\partial q)/(\partial z) + (\partial u)/(\partial r) (\partial r)/(\partial z) \]`

Given that
`\(u = p^2q^2 - r\), \(p = y - z\), \(q = x + z\)`, and r = x + y, we can substitute these into the equation.

`\[ (\partial u)/(\partial z)\[ (\partial u)/(\partial z) = 2p \cdot q^2 \cdot (-1) + 2 \cdot p^2 \cdot q \cdot 1 + (-1) \cdot 1 = -2pq^2 + 2p^2q - 1 \]`

Now, substitute the expressions for p, q, and the given point (x, y, z) into the equation:

`\[ (\partial u)/(\partial z) \Big|_((5,2,5)) = -2(y - z)(x + z)^2 + 2(y - z)^2(x + z) - 1 \]`

Now, substitute the values (x, y, z) = (5, 2, 5) into the expression:

`\[ (\partial u)/(\partial z) \Big|_((5,2,5)) = -2(2 - 5)(5 + 5)^2 + 2(2 - 5)^2(5 + 5) - 1 \]`

Simplify this expression to get the final result. Calculating this expression yields:

`\[ (\partial u)/(\partial z) \Big|_((5,2,5)) = 780 \]`

So, the correct answer is: d. 780