Question

Elena loves to go fishing. Each time she catches a fish, there is a 70% chance that it is a northern pike and a 30% chance it is a walleye. Let X be the random variable that represents the number of northern pike Elena gets if she catches 2 fish. Find the expected value of the number of northern pike Elena catches?

Answer 1

Expected number of northern pike Elena catches: 1.4

1. Identifying the Scenario:

We know Elena catches fish, and each catch has a 70% chance of being a northern pike (X) and 30% chance of being a walleye.

We want to find the expected value of X, which is the average number of northern pike she catches, if she catches 2 fish.

2. Setting Up the Probability Distribution:

Since each catch is independent, the probability of catching X northern pike in 2 fish is a binomial distribution.

The binomial distribution formula for probability is: P(X = k) = (n choose k)
`* p^k * (1-p)^(n-k)`

where:

n = total catches = 2

k = number of northern pike = X (value we're calculating)

p = probability of catching a northern pike = 0.7

(n choose k) is the binomial coefficient, representing the number of ways to get k successes in n trials.

3. Calculating Expected Value:

The expected value of a random variable is the average of its possible outcomes weighted by their probabilities.

For the binomial distribution, the expected value formula is: E(X) = n * p where:

n and p are the same as before.

4. Applying the Formulas:

For X = 0 (no northern pike):
`P(X = 0) = (2 choose 0) * 0.3^2 * 0.7^0 = 0.09`

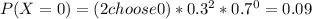
For X = 1 (1 northern pike): P(X = 1) =
`(2 choose 1) * 0.7^1 * 0.3^1 = 0.28`

For X = 2 (2 northern pike): P(X = 2) =
`(2 choose 2) * 0.7^2 * 0.3^0 = 0.49`

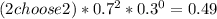
Expected Value (E(X)) = 2 * 0.7 = 1.4

5. Conclusion:

On average, Elena can expect to catch 1.4 northern pike if she catches 2 fish.