Question

What is the partial fraction decomposition of startfraction 6x+17/(x+1)²?

a. 6x+17/(x+1)²=6/x+1 + 11/(x+1)²
b. 6x+17/(x+1)²=6/x+1 + 17/(x+1)²
c. 6x+17/(x+1)²=6/x+1 - 11/(x+1)²
d. 6x+17/(x+1)²=6/x+1 - 17/(x+1)²

Answer 1

The correct answer is a. 6x+17/(x+1)²=6/x+1 + 11/(x+1)².

To perform partial fraction decomposition on
`(6x+17)/((x+1)^2)` , let's express it in the form of
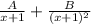`(A)/(x+1) + (B)/((x+1)^2)` where A and B are constants to be determined.

`(6x+17)/((x+1)^2) =`
`(A)/(x+1) + (B)/((x+1)^2)`

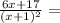
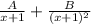
​To find A and B, we can start by multiplying through by the denominator (x+1)^2:

6x+17=A(x+1)+B

Now, let's solve for A and B.

Expanding the right-hand side:

6x+17=Ax+A+B

To equate coefficients of like terms:

Coefficient of x:

6x=Ax⟹A=6

Constant term:

17=A+B⟹B=17−A=17−6=11

Therefore, the partial fraction decomposition is:

`(6x+17)/((x+1)^2) = (6)/(x+1) +(11)/((x+1)^2)`

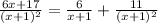
​So, the correct answer is a.6x+17/(x+1)²=6/x+1 + 11/(x+1)²