Question

John

and
Harry
take
part
in
running
competitions.
John's
mass
is
half
the
mass
of
Harry
and
John's
speed
is
4
times
greater
than
that
of
Harry.
By
how
much
must
Harry
speed
up
if
he
wants
to
have
the
same
kinetic
energy
as
John?
Harry's
original
speed
is
4m/s
Give
your
answer
to
2
decimal
places.

Answer 1

Harry needs to speed up by 1.66 m/s to match John's kinetic energy.

The kinetic energy (KE) of an object is given by the formula:

`$ KE = (1)/(2) m v^2 $$`

where m is the mass and v is the speed of the object.

Given that John's mass is half the mass of Harry and John's speed is 4 times greater than that of Harry, the kinetic energy of John is:

`$$ KE_{\text{John}} = (1)/(2) * (1)/(2)m * (4v)^2 = 4 * (1)/(2) m v^2 = 2 KE_{\text{Harry}} $$`

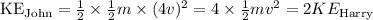
So, John's kinetic energy is twice that of Harry's.

If Harry wants to have the same kinetic energy as John, he needs to increase his kinetic energy by a factor of 2. We can achieve this by increasing his speed. Let's denote Harry's new speed as v'. Then we have:

`$$ 2 KE_{\text{Harry}} = (1)/(2) m (v')^2 $$`

Solving for v' gives:

`$ v' = √(2) v $$`

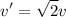
Substituting Harry's original speed v = 4 m/s into the equation gives:

`$$ v' = √(2) * 4 \, \text{m/s} \approx 5.66 \, \text{m/s} $$`

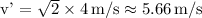
So, Harry needs to increase his speed to approximately 5.66 m/s to have the same kinetic energy as John.

`\(5.66 \, \text{m/s} - 4 \, \text{m/s} = 1.66 \, \text{m/s}\)`

This means Harry needs to speed up by 1.66 m/s to match John's kinetic energy.