Question

If ABCD is a rhombus AC-18, and the perimeter of ABCD is 52, find BD. ​

Answer 1

Answer:
`4√(22)`

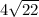
This is approximately equal to 18.76166 units.

========================================================

Step-by-step explanation

A rhombus has all four sides the same length.

The perimeter is 52 units, so each side of the rhombus is 52/4 = 13 units long.

I'm assuming you meant to say AC = 18. If so, then the diagonals of the rhombus bisect each other at point E, which lead to AE = 9 and EC = 9.

Focus on one of the smaller right triangles. Let's say we focus on right triangle AEB.

The known leg is AE = 9. The unknown leg EB is x. Hypotenuse AB is 13 units long.

Use the Pythagorean theorem
`a^2+b^2 = c^2` and it leads to the equation
`9^2+x^2 = 13^2`. Skipping a bit of steps, that equation solves to
`x = 2√(22)`

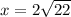
Therefore
`EB = 2√(22) \ \text{ and } BD = 2*EB = 2*2√(22) = 4√(22)`

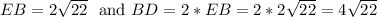
Side note:
`4√(22) \approx 18.76166`