Question

Match the steps to factor the equation by grouping. 10x2 + 11x + 3 1. 10x2 + 5x + 6x + 3 Selected:e. Step 1This answer is incorrect. 2. Choose the correct factors of 30 that add to 11 Selected:c. Step 2This answer is correct. 3. 10 * 3 = 30 Selected:a. Step 5This answer is incorrect. 4. (5x + 3)(2x + 1) Selected:b. Step 4This answer is incorrect. 5. 5x(2x + 1) + 3(2x + 1) Selected:d. Step 3This answer is incorrect.

Answer 1

To factor the quadratic equation
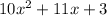`10x^2 + 11x + 3` by grouping, first find two numbers that multiply to 30 and add up to 11, then rewrite the middle term, group the terms, factor out common factors, and finally, factor out the binomial to get
`(5x + 3)(2x + 1)`.

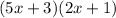Factoring by grouping involves several steps to simplify a quadratic equation. The given equation is
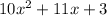`10x^2 + 11x + 3`. To factor this equation, we need to follow the correct sequence of steps for factoring by grouping:

1. Find a pair of numbers that multiply to give the product of the coefficient of the
   `x^2` term and the constant term, which should also add up to the coefficient of the x term. In this case,
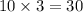   `10 * 3 = 30`, and we need two numbers that multiply to 30 and add up to 11.
2. Once the pair (5, 6) is found, rewrite the middle term (11x) as the sum of two terms using the found numbers:
   `10x^2 + 5x + 6x + 3`.
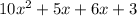3. Group the terms in pairs:
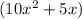   `(10x^2 + 5x)` and
   `(6x + 3)`.
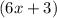4. Factor out the common factors from each pair:
   `5x(2x + 1) + 3(2x + 1)`
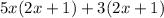
5. Since the same binomial appears in both terms, factor it out to get the final factored form:
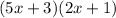   `(5x + 3)(2x + 1)`.