The straight-line equation for the graph that passes through p₁ (-3, 3) and p² (1, 0) is: y = -3/4x + 3/4.
What is the straight-line equation?
To find the equation of the straight line passing through points
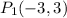 and
and
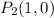 , you can use the slope-intercept form of the equation for a line:
, you can use the slope-intercept form of the equation for a line:
y = mx + b.
First, calculate the slope (m) using the formula:
![\[m = \frac{{y_2 - y_1}}{{x_2 - x_1}}.\]](https://img.qammunity.org/2024/formulas/mathematics/college/tkkbww4buf9gcvqd7wt594z0ljy6j5wn8c.png)
For the points
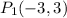 and
and
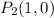 :
:
![\[m = \frac{{0 - 3}}{{1 - (-3)}} = \frac{{-3}}{{4}}.\]](https://img.qammunity.org/2024/formulas/mathematics/college/e394burw25uotz1e8dp0jb14sycajzzbnl.png)
Now that you have the slope (m), you can use one of the given points to find the y-intercept (b). Let's use
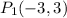 :
:
![\[3 = \frac{{-3}}{{4}} \cdot (-3) + b.\]](https://img.qammunity.org/2024/formulas/mathematics/college/sm321rxf9mp70dswc44jbdsryf32e1ybnc.png)
Solving for b:
3 = 9/4 + b
b = 3 - 9/4
b = 3/4
Now, you have the slope (m = -3/4) and the y-intercept (b = 3/4), so the equation of the line is:
y = -3/4x + 3/4.