Question

Is the point (2,1) a solution

Answer 1

Substituting x=2 and y=1 into the equation
`\(3x - 2y = 4\)` results in
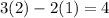`\(3(2) - 2(1) = 4\)`. As the equation holds true, (2,1) is a solution.

To check if the point (2,1) is a solution to the equation
`\(3x - 2y = 4\)`, substitute
`\(x = 2\)` and
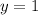`\(y = 1\)` into the equation. Begin by replacing \(x\) with \(2\) and
`\(y\)` with
`\(1\)`:

`\[3(2) - 2(1) = 6 - 2 = 4\]`

Upon calculation, the equation simplifies to
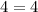`\(4 = 4\)`. Since the left-hand side (LHS) equals the right-hand side (RHS), the point (2,1) satisfies the equation. Therefore, (2,1) is indeed a solution to
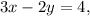`\(3x - 2y = 4\),` confirming that when
`\(x = 2\)` and
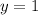`\(y = 1\)` , the equation holds true.

completed question:

"Given the equation
`\(3x - 2y = 4\)` , determine whether the point (2,1) is a solution to the equation. If yes, verify by substituting the x-coordinate as
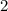`\(2\)` and the y-coordinate as
`\(1\)` into the equation and check whether the resulting equation holds true."