Question

Vec A = 4i vec B = - 4i angle of vec A + vec B with x-axis is equal to

Answer 1

The angle of
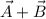`\( \vec{A} + \vec{B} \)` with the x-axis is 315°.

The vectors A and B are given as
`\( \vec{A} = 4\hat{i} \) and \( \vec{B} = -4\hat{j} \)`.

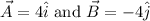The sum of the vectors A and B is
`\( \vec{A} + \vec{B} = 4\hat{i} - 4\hat{j} \)`.

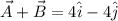The angle θ that a vector makes with the positive x-axis can be found using the formula¹²³:

`$ \theta = \arctan\left((y)/(x)\right) $$`

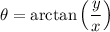
where x and y are the components of the vector. For the vector
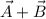`\( \vec{A} + \vec{B} \)`, x = 4 and y = -4. So,

`$ \theta = \arctan\left((-4)/(4)\right) = \arctan(-1) $$`

The arctangent of -1 is -45 degrees, but since we're measuring the angle counterclockwise from the positive x-axis, we add 360 degrees to get a positive angle:

`$$ \theta = -45^o + 360^o = 315^o $$`

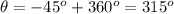
So, the angle of
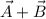`\( \vec{A} + \vec{B} \)` with the x-axis is 315°.