Question

A fisher has anchored their 11 m long boat far away from the shore. The waves in the water cause the boat to rock, and the boat performs 11 vertical oscillations within 9 s . The wave crests travel from bow (front) to stern (back) of the boat in 4 s . They notice that at time t = 0 the bow of the boat is at the top of a wave. They then observe the wave phase at bow again at t=1 s t0 t1 s What is the period of waves? T= 9/11 s Your last answer was interpreted as follows: 911 What is the wavelength? λ= 2.249 m Your last answer was interpreted as follows: 2.249 What is the number of complete waves that fits in the length of the boat simultaneously? nwaves= 4 Your last answer was interpreted as follows: 4 What is the angular velocity of the waves? ω= 22*pi/9 rads Your last answer was interpreted as follows: 22π9 What is the wave phase at the time of the second observation [0...2 pi]? ϕ= rad

Answer 1

The waves have a period of 9/11 s, wavelength of 2.249 m, and angular velocity of 22π/9 rad/s. Four complete waves fit in the 11 m boat, and at t=1s, the wave phase is 22π/9 rad.

Let's break down the information given:

1. **Period of waves (T):** The period is the time it takes for one complete oscillation. In this case, T is given as 9/11 s.

`\[ T = (9)/(11) \, \text{s} \]`

2. **Wavelength (λ):** The wavelength is the distance between two consecutive wave crests. The given value is λ = 2.249 m.

`\[ \lambda = 2.249 \, \text{m} \]`

3. **Number of complete waves that fit in the length of the boat simultaneously (nwaves):** The boat is 11 m long, and nwaves is given as 4.

`\[ nwaves = 4 \]`

4. **Angular velocity of the waves (ω):** Angular velocity is related to the period by the formula
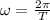`\( \omega = (2\pi)/(T) \)`. Substituting the given period value:

`\[ \omega = (2\pi)/((9)/(11)) \, \text{rad/s} \]`

5. **Wave phase at the time of the second observation (ϕ):** The wave phase can be calculated using the formula
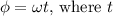`\( \phi = \omega t \), where \( t \)` is the time of observation. In this case, \( t = 1 \) s.

Now, let's calculate these values:

1. Calculate \( \omega \):

`\[ \omega = (2\pi)/((9)/(11)) \, \text{rad/s} \]`

`\[ \omega = (22\pi)/(9) \, \text{rad/s} \]`

2. Calculate \( \phi \):

`\[ \phi = \omega t \]`

`\[ \phi = (22\pi)/(9) * 1 \, \text{rad} \]`

The final answers are:

- Period of waves
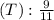`(T): \( (9)/(11) \)` s

- Wavelength (λ): 2.249 m

- Number of complete waves
`(nwaves):`4

- Angular velocity of waves (ω):
`\( (22\pi)/(9) \) rad/s`

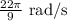
- Wave phase at the time of the second observation (ϕ):
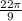`\( (22\pi)/(9) \)`rad