Question

You want to be able to withdraw $30,000 from your account each year for 25 years after you retire.

You expect to retire in 20 years.

If your account earns 9% interest, how much will you need to deposit each year until retirement to achieve your retirement goals?

$

Round your answer to the nearest cent.

Answer 1

$5,759.90

Explanation:

First, we need to calculate how much money should be accumulated in the account during the 20 years prior to retiring in order to have enough to withdraw $30,000 at the beginning of each year for 25 years after retiring. To calculate this, we can use the payout annuity formula.

`P_0=(w\left(1-\left(1+(r)/(k)\right)^(-Nk)\right))/(\left((r)/(k)\right))`

where:

• P₀ is the balance in the account at the beginning.
• w is the regular withdrawal (the planned amount to withdraw each time period).
• r is the annual interest rate (in decimal form).
• k is the number of compounding periods in one year.
• N is the number of years to take withdrawals.

In this case:

• w = $30,000
• r = 9% = 0.09
• k = 1 (assuming the interest compounds annually)
• N = 25 years

Substituting the values into the formula gives:

`P_0=(30000\left(1-\left(1+(0.09)/(1)\right)^(-25 \cdot 1)\right))/(\left((0.09)/(1)\right))`

`P_0=(30000\left(1-\left(1.09\right)^(-25)\right))/(0.09)`

`P_0=294677.39`

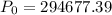
Therefore, the balance of the account at the beginning of retirement needs to be $294,677.39.

Now, to calculate how much we need to deposit at the end of each year for the duration of 20 years before retirement to achieve the required initial retirement balance of $294,677.39, we can use the savings annuity formula:

`P_N=(d\left(\left(1+(r)/(k)\right)^(Nk)-1\right))/(\left((r)/(k)\right))`

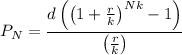
where:

• 
  `P_N` is the balance in the account after N years.
• d is the regular deposit amount (the planned amount to deposit each time period).
• r is the annual interest rate (in decimal form).
• k is the number of compounding periods in one year.
• N is the number of years .

In this case:

• 
  `P_N` = $294,677.39
• r = 9% = 0.09
• k = 1 (assuming the interest compounds annually)
• N = 20 years

Substituting the values into the formula gives:

`294677.39=(d\left(\left(1+(0.09)/(1)\right)^(20 \cdot 1)-1\right))/(\left((0.09)/(1)\right))`

`294677.39=(d\left(\left(1.09\right)^(20)-1\right))/(0.09)`

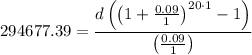
Solve for d:

`26520.97=d\left(\left(1.09\right)^(20)-1\right)`

`d=(26520.97)/(\left(1.09\right)^(20)-1)`

`d=5759.90`

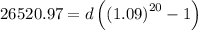
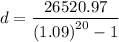
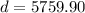
Therefore, the amount needed to be deposited at the end of each year to achieve the given retirement goals is $5,759.90.