Can the polynomial 82x^12y^6 + 14 - 18x^12y^6-13 be factored using aun of cubes, different of cubes , or neither?

Question

asked Aug 12, 2024 157k views

1 Answer

Yanki · Answer 1 · 2024-08-17T13:16:41+0000

The polynomial
$82x^(12)y^6 + 14 - 18x^(12)y^6 - 13$ can be factored using the sum of cubes formula. The factored form is:

$\[(4x^4y^2 + 1)((4x^4y^2)^2 - 4x^4y^2 + 1)\].$

First, rewrite the polynomial by grouping like terms:

$(82x^(12)y^6 - 18x^(12)y^6) + (14 - 13)$

Combine the terms involving
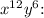
$$x^(12)y^6$:$

$64x^(12)y^6 + 1$

Now, let's reconsider the expression
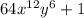$64x^(12)y^6 + 1$ . It doesn't directly fit the form of a sum of cubes
$($a^3 + b^3$)$ , as there are no cube terms. However, we can express it as
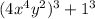$(4x^4y^2)^3 + 1^3$ , which allows us to apply the sum of cubes formula
$($a^3 + b^3 = (a + b)(a^2 - ab + b^2)$)$ .