Question

22. The photon emitted by a cyclotron has a velocity of 1.50 × 10³ m/s. What is the wavelength of this photon? Given that the mass of photon = 1.676 × 10-27 kg and Planck's constant = 6.62 × 10-34 J.S. 23. Calculate the wavelength of the light emitted when an electron falls from n = 3 to the n = 1 state in hydrogen atom. 24. Write the number and the letter for the orbital that corresponds to the following pairs of n and I quantum numbers: a. n = 3, 1=1 cn=3,1=2 b. n = 4,7 = 0dn = 5, 7 = 3 25. What type of orbital (i.e. 3s, 4p, ...) is designated by these quantum numbers? b. n = 4, {=2, m, = -2 a. n=5₁ € = 1, m, = 0 c. n = 2, {=0, m₁ = 0 26. Write the ground-state electron configurations for the following elements: a. Br (Z = 35) b. Mo (Z = 42) c. W (Z = 74) 27. Write the period number for each of the following and state if they are metal, nonmetal or metalloid: a. P b. Ge d. n = 4, C = 3, m = -3 c. F d. W​

Answer 1

The kinetic energy of a particle with a mass of
`\(2.0 * 10^(-26) \, \text{kg}\) and velocity \(5.0 * 10^3 \, \text{m/s}\) is \(25 * 10^(-20) \, \text{J}\), calculated using \(KE = (1)/(2)mv^2\).`

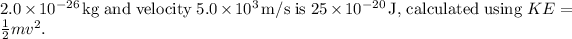
To find the kinetic energy (KE) of the particle, you can use the formula:

`\[ KE = (1)/(2)mv^2 \]`

where:

-
`\( m \)`is the mass of the particle,

-
`\( v \)`is the velocity of the particle.

Given:

-
`\( m = 2.0 * 10^(-26) \, \text{kg} \)` (mass of the particle),

-
`\( v = 5.0 * 10^3 \, \text{m/s} \)` (velocity of the particle).

Plug in these values into the formula:

`\[ KE = (1)/(2) * (2.0 * 10^(-26) \, \text{kg}) * (5.0 * 10^3 \, \text{m/s})^2 \]`

Calculate the result:

`\[ KE = (1)/(2) * (2.0 * 10^(-26)) * (25 * 10^6) \, \text{J} \]`

`\[ KE = 0.5 * (2.0 * 10^(-26)) * (25 * 10^6) \, \text{J} \]`

`\[ KE = 25 * 10^(-26) * 10^6 \, \text{J} \]`

`\[ KE = 25 * 10^(-20) \, \text{J} \]`

So, the kinetic energy of the particle is
`\( 25 * 10^(-20) \, \text{J} \).`

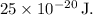
THE probable question maybe:

28. A particle with a mass of 2.0 × 10^-26 kg is moving with a velocity of 5.0 × 10^3 m/s. Determine the kinetic energy of the particle using the formula \( KE = \frac{1}{2}mv^2 \). Given that Planck's constant is \( h = 6.62 \times 10^{-34} \, J \cdot s \).

(Note: You can use this information to calculate the kinetic energy of the particle.)