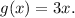After the specified transformations, the equation for
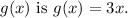
Given that the graph of
 is a transformation of the graph of
is a transformation of the graph of
 involving a horizontal compression by a factor of
involving a horizontal compression by a factor of
 followed by a vertical stretch by a factor of 2, the equation for
followed by a vertical stretch by a factor of 2, the equation for
 can be obtained as follows:
can be obtained as follows:
1. Horizontal Compression by
 : Multiply the variable
: Multiply the variable
 by
by
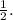
![\[ f_1(x) = 3 \left((1)/(2)x\right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/bi0xb0qrr1o668rwscofpsidda3v0vlq7c.png)
2. Vertical Stretch by 2: Multiply the entire function by 2.
![\[ g(x) = 2 \cdot f_1(x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/zbl30mgt9vdeztplm2hz5qtxjzhap5nyd9.png)
Combine these steps:
![\[ g(x) = 2 \cdot 3 \left((1)/(2)x\right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/xa96gx9k9iiqkfhdvppay0h7fk7kz9fj24.png)
Simplify further:
![\[ g(x) = 3x \]](https://img.qammunity.org/2024/formulas/mathematics/college/m52r5aes0vm4z3grwzwrt1hg971c47vi87.png)
Therefore, after the specified transformations, the equation for
 is
is