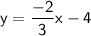Question

Find the equation for the line.
4-3-2-10
Oy=x-4
Oy=²x-4
Oy=x+4
Oy=x+4

Answer 1

`\sf y = (-2)/(3)x - 4`

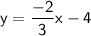
Explanation:

To find the equation of a line.

Let's take two points:

(-3,-2) and (0,-4)

Now, we can use the slope-intercept form of a linear equation, which is given by:

`\sf y = mx + b`

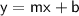
where

• m is the slope and
• b is the y-intercept.

First, calculate the slope ( m ) using the formula:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

Let's use the points (-3, -2) and (0, -4):

`\sf m = ((-4 - (-2)))/((0 - (-3)))`

`\sf m = (-4 + 2)/(3)`

`\sf m = (-2)/(3)`

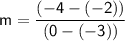
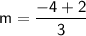
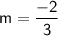
Now that we have the slope
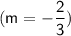`\sf (m = -(2)/(3) )`, we can use one of the points (let's use (-3, -2)) to find the y-intercept ( b ).

Substitute the values into the equation:

`\sf -2 = -(2)/(3) * (-3) + b`

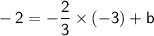
Simplify:

`\sf -2 = 2 + b`

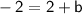
Subtract 2 from both sides:

`\sf -2-2 = 2 + b -2`

`\sf b = -4`

Now we have the slope
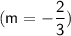`\sf ( m = -(2)/(3) )` and the y-intercept ( b = -4 ), so we can write the equation of the line:

`\sf y = (-2)/(3)x - 4`

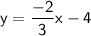
Therefore, the equation of the line is:

`\sf y = (-2)/(3)x - 4`