Player A is more consistent, and the correct statement is "Player A is the most consistent, with a standard deviation of 1.4."
How did we arrive at this assertion?
To determine which player is more consistent, you would typically look at the measure of variability. In this case, the standard deviation is a commonly used measure of variability.
Calculate the standard deviation for both players:
Player A:
![\[ \text{Mean (}\(x-bar}\text{)} = (2 + 3 + 1 + 3 + 2 + 2 + 1 + 3 + 6)/(9) = (23)/(9) \approx 2.56 \]](https://img.qammunity.org/2024/formulas/mathematics/college/7ar3jfj1rn7asxcz3br05j9hnz3kywom8l.png)
![\[ \text{Squared differences from the mean: } (2-2.56)^2, (3-2.56)^2, \ldots, (6-2.56)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/adfy46e6ce5rly3r2ing96lztq4yomwqjw.png)
![\[ \text{Sum of squared differences: } 0.3136 + 0.1936 + 2.4336 + 0.1936 + 0.3136 + 0.3136 + 2.4336 + 0.1936 + 11.8336 = 18.2224 \]](https://img.qammunity.org/2024/formulas/mathematics/college/23s8arwttj1g3sr542ox6zajmcuz6dwqol.png)
![\[ \text{Variance (}\sigma^2\text{)} = (18.2224)/(9) \approx 2.025 \]](https://img.qammunity.org/2024/formulas/mathematics/college/capctval8r77xib4c4jpwcb6lvszh4as3c.png)
![\[ \text{Standard Deviation (}\sigma\text{)} \approx √(2.025) \approx 1.4230 \]](https://img.qammunity.org/2024/formulas/mathematics/college/e1fg40sgfkd9vwjsh6c64kcxkrbcjgw0k2.png)
Player B:
![\[ \text{Mean (}\bar{x}\text{)} = (2 + 1 + 3 + 8 + 2 + 1 + 4 + 3 + 1)/(9) = (25)/(9) \approx 2.78 \]](https://img.qammunity.org/2024/formulas/mathematics/college/c83xhltaqx4a957ion6mm38p9zvx0su5la.png)
![\[ \text{Squared differences from the mean: } (2-2.78)^2, (1-2.78)^2, \ldots, (1-2.78)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/6z6lagigyky29aa5sj2ndlwnc20kc5fmnt.png)
![\[ \text{Sum of squared differences: } 0.6084 + 3.1684 + 0.0484 + 27.2484 + 0.6084 + 3.1684 + 1.4884 + 0.0484 + 3.1684 = 39.5556 \]](https://img.qammunity.org/2024/formulas/mathematics/college/l0qy2r6mscqawhmf9hqxq6s5h5m6ipwvvs.png)
![\[ \text{Variance (}\sigma^2\text{)} = (39.5556)/(9) \approx 4.3951 \]](https://img.qammunity.org/2024/formulas/mathematics/college/1hgy4rds8jkbchzmu15dn37wooqojjzrze.png)
![\[ \text{Standard Deviation (}\sigma\text{)} \approx √(4.3951) \approx 2.0964 \]](https://img.qammunity.org/2024/formulas/mathematics/college/q0uv11mamvzx4o9v6f6958zdgbda26cyo5.png)
Comparing the standard deviations:
- Player A:
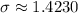
- Player B:
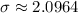
Therefore, Player A is more consistent, and the correct statement is:
• Player A is the most consistent, with a standard deviation of 1.4.